Algorithms and Data Structures in C++ by Alan Parker CRC Press, CRC Press LLC ISBN: 0849371716   Pub Date: 08/01/93

1.4 Putting it All Together

This section presents an example combining ASCII, floating point, and integer types using one final C++ program. The program is shown in Code List 1.15 and the output is shown in Code List 1.16.

The program utilizes a common memory location to store 8 bytes of data. The data will be treated as double, float, char, int, or long. A particular memory implementation for this program is shown in Figure 1.2.

Figure 1.2  Memory Implementation for Variable t

Figure 1.3  Mapping of each Union Entry

The organization of each union entry is shown in Figure 1.3. For the union declaration t there are only eight bytes stored in memory. These eight bytes can be interpreted as eight individual characters or two longs or two doubles, etc. For instance by looking at Table 1.8 one sees the value of ch[0] which is 0×41 which is the letter A. Similarly, the value of ch[1] is 0×42 which is the letter B. When interpreted as an integer the value of i[0] is 0×41424344 which is in 2’s complement format. Converting to decimal one has i[0] with the value of

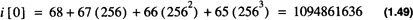
If one were to interpret 0×41424344 as an IEEE 32-bit floating point number its value would be 12.1414. If one were to interpret 0×45464748 as an IEEE 32-bit floating point number its value would be 3172.46.

Code List 1.15 Data Representations

Code List 1.16 Output of Program in Code List 1.15

There are only one’s and zero’s stored in memory and collections of bits can be interpreted to be characters or integers or floating point numbers. To determine which kind of operations to perform the compiler must be able to determine the type of each operation.

1.5 Problems

(1.1)  Represent the following decimal numbers when possible in the format specified. 125, -1000, 267, 45, 0, 2500. Generate all answers in HEX!

a)  8-bit 2’s complement—2 hex digits

b)  16-bit 2’s complement—4 hex digits

c)  32-bit 2’s complement—8 hex digits

d)  64-bit 2’s complement—16 hex digits

(1.2)  Convert the 12-bit 2’s complement numbers that follows to 32-bit 2’s complement numbers. Present your answer with 8 hex digits.

a)  0xFA4

b)  0x802

c)  0x400

d)  0x0FF

(1.3)  Represent decimal 0.35 in IEEE 32-bit format and IEEE 64-bit format.

(1.4)  Represent the decimal fraction 4/7 in binary.

(1.5)  Represent the decimal fraction 0.3 in octal.

(1.6)  Represent the decimal fraction 0.85 in hex.

(1.7)  Calculate the floating point number represented by the IEEE 32-bit representation F8080000.

(1.8)  Calculate the floating point number represented by the IEEE 64-bit representation F808000000000000.

(1.9)  Write down the ASCII representation for the string “Hello, how are you?”. Strings in C++ are terminated with a 00 in hex (a null character). Terminate your string with the null character. Do not represent the quotes in your string. The quotes in C++ are used to indicate the enclosure is a string.

(1.10)  Write a C++ program that outputs “Hello World”.

(1.11)  In Code List 1.8 the twos complement of the largest representable negative integer, -32768, is the same number. Explain this result. Is the theory developed incorrect?

(1.12)  In Section 1.1.4 the issue of conversion is assessed for signed-magnitude, unsigned, and 2’s complement numbers. Is there a simple algorithm to convert an IEEE 32-bit floating point number to IEEE 64-bit floating point number?