Algorithms and Data Structures in C++ by Alan Parker CRC Press, CRC Press LLC ISBN: 0849371716   Pub Date: 08/01/93

2.2 Induction

Simple induction is a two step process:

•  Establish the result for the case N = 1

•  Show that if is true for the case N = n then it is true for the case N = n+1

This will establish the result for all n > 1.

Induction can be established for any set which is well ordered. A well-ordered set, S, has the property that if

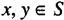
then either

•  x<y

•  x>y or

•  x = y

Example 2.4  Order

Additionally, if S′ is a nonempty subset of S:

then S′ has a least element. An example of simple induction is shown in Example 2.5.

The well-ordering property is required for the inductive property to work. For example consider the method of infinite descent which uses an inductive type approach. In this method it is required to demonstrate that a specific property cannot hold for a positive integer. The approach is as follows:

Example 2.5  Induction

1.  Let P (k) = TRUE denote that a property holds for the value of k. Also assume that P(0) does not hold so P(0) = FALSE.

Let S be the set that

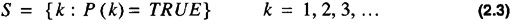
From the well-ordering principle it is true that if S is not empty then S has a smallest member. Let j be such a member:

2.  Prove that P(j) implies P(j-1) and this will lead to a contradiction since P(0) is FALSE and j was assumed to be minimal so that S must be empty. This implies the property does not hold for any positive integer k. See Problem 2.1 for a demonstration of infinite descent.

2.3 Recursion

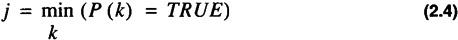
Recursion is a powerful technique for defining an algorithm.

Definition 2.6

A procedure is recursive if it is, whether directly or indirectly, defined in terms of itself.

2.3.1 Factorial

One of the simplest examples of recursion is the factorial function f(n) = n!. This function can be defined recursively as

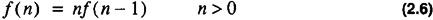
A simple C++ program implementing the factorial function recursively is shown in Code List 2.1. The output of the program is shown in Code List 2.2.

Code List 2.1 Factorial

Code List 2.2 Output of Program in Code List 2.1

2.3.2 Fibonacci Numbers

The Fibonacci sequence, F(n), is defined recursively by the recurrence relation

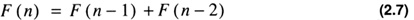
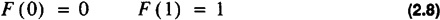
A simple program which implements the Fibonacci sequence recursively is shown in Code List 2.3. The output of the program is shown in Code List 2.4.

Code List 2.3 Fibonacci Sequence Generation

Code List 2.4 Output of Program in Code List 2.3

The recursive implementation need not be the only solution. For instance in looking for a closed solution to the relation if one assumes the form F (n) = λⁿ one has

which assuming λ ≠ 0

The solution via the quadratic formula yields

Because Eq. 2.7 is linear it admits solutions of the form

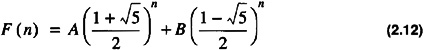
To satisfy the boundary conditions in Eq. 2.8 one obtains the matrix form

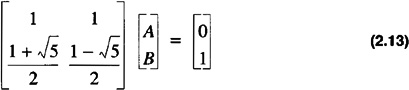
multiplying both sides by the 2 × 2 matrix inverse

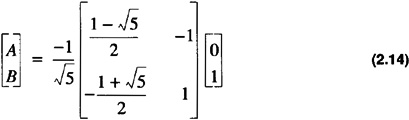
which yields

resulting in the closed form solution

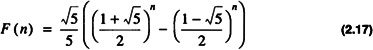
A nonrecursive implementation of the Fibonacci series is shown in Code List 2.5. The output of the program is the same as the recursive program given in Code List 2.4.

Code List 2.5 Fibonacci Program — Non Recursive Solution

2.3.3 General Recurrence Relations

This section presents the methodology to handle general 2nd order recurrence relations. The recurrence relation given by

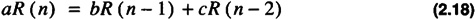
with initial conditions:

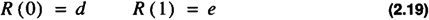
can be solved by assuming a solution of the form R (n) = λⁿ. This yields

If the equation has two distinct roots, λ₁,λ₂, then the solution is of the form

where the constants, C₁, C₂, are chosen to enforce Eq. 2.19. If the roots, however, are not distinct then an alternate solution is sought:

where λ is the double root of the equation. To see that the term C₁nλⁿ satisfies the recurrence relation one should note that for the multiple root Eq. 2.18 can be written in the form

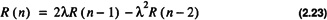
Substituting C₁nλⁿ into Eq. 2.23 and simplifying verifies the solution.