Algorithms and Data Structures in C++ by Alan Parker CRC Press, CRC Press LLC ISBN: 0849371716   Pub Date: 08/01/93

2.7 Problems

(2.1)  [Infinite Descent — Difficult] Prove, using infinite descent, that there are no solutions in the positive integers to

(2.2)  [Recuffence] Find the closed form solution to the recursion relation

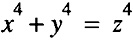
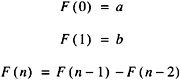
and write a C++ program to calculate the series via the closed form solution and print out the first twenty terms of the series for

(2.3)  [Tower of Hanoi] Write a C++ Program to solve the Tower of Hanoi problem for arbitrary n. This program should output the move sequence for a specific solution.

(2.4)  [Tower of Hanoi] Is the minimal solution to the Tower of Hanoi problem unique? Prove or disprove your answer.

(2.5)  [Rectangular Mesh] Given an 8x8 rectangular mesh with no additional edge connections calculate the largest distance between two processors, where the distance is defined as the minimum number of edges to traverse in a path connecting the two processors.

(2.6)  [Rectangular Mesh] For a rectangular mesh with no additional edge connections formally describe the topology in terms of vertices and edges.

(2.7)  [Rectangular Mesh] Write a C++ program to generate a PostScript image file of the rectangular mesh for 1 ≤ n ≤ 20 without additional external edge connections. To draw a line from the current point to (x, y) use the primitive

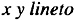
followed by

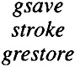
to actually draw the line. Test the output by sending the output to a PostScript printer.

(2.8)  [Cube-Connected Cycles] Calculate the number of edges in a cube connected cycles topology with nlog n nodes.

(2.9)  [Tree Structure] For a graph G, which is a tree, prove that

(2.10)  [Cube-Connected Cycles] For a cube-connected cycles topology formally describe the topology in terms of vertices and edges.

(2.11)  [Hypercube] Given two arbitrary nodes in a hypercube of dimension n calculate the number of distinct shortest paths which connect two distinct nodes, A and B, as a function of the two nodes. Use a binary representation for each of the nodes:

(2.12)  [Hypercube] Given a hypercube graph of dimension n and two processors A and B what is the minimum number of edges that can be removed such that there is no path from A to B.

(2.13)  Is every edge in a tree a bridge?

(2.14)  Devise a broadcast algorithm for a hypercube of arbitrary dimension. Write a C++ program to simulate this broadcast operation on an 8-dimensional hypercube.

(2.15)  Devise a message passing algorithm for a hypercube of arbitrary dimension. Write a C++ program to simulate this algorithm and demonstrate it for a 12-dimensional hypercube.

(2.16)  Write a C++ program to visualize a complete binary tree. Your program should scale the node sizes to fit on the page as a function of the dimension in a similar fashion to Code List 2.10.

(2.17)  Describe in detail the function of each procedure in the code to visualize the hypercube in Code List 2.10. Present a high-level description of the procedures render_cube and init_cube.

(2.18)  Write a C++ program to display the modified adjacency matrix of an n-dimensional hypercube similar to the matrix presented in Eq. 2.67.

(2.19)  Write a C++ program to visualize a 64-node hypercube which supports message passing. Your program should use a separate gray level to draw the source and destination processors and should draw the edges which form the path in a different gray scale also.

(2.20)  [Difficult] Prove that the modified message passing algorithm works for any two functional processors in an efficient hypercube.

(2.21)  Write a C++ program to determine if a hypercube with failed nodes is efficient.

(2.22)  Calculate the least-weighted path-length matrix for each of the subcubes in Figure 2.20.

(2.23)  Given a hypercube of dimension d calculate the probability that a subcube is efficient where the subcube is formed by the random failure of two processors.

(2.24)  Modify the C++ program in Code List 2.10 to change the line width relative to the node size. Test out the program for small and high dimensions.

(2.25)  Rewrite Code List 2.10 to build the hypercube using a recursive function.

(2.26)  The program in Code List 2.10 uses a simple algorithm to draw a line from each processor node to its neighbors. As a result, the edges are drawn multiple times within in the file. Rewrite the program to draw each line only once.