Algorithms and Data Structures in C++ by Alan Parker CRC Press, CRC Press LLC ISBN: 0849371716   Pub Date: 08/01/93

4.4.3 Shifting over 1’s and 0’s

If the divisor is normalized so that it begins with a 1 then the technique of the previous sections can be improved to skip over 1’s and 0’s. Shifting over 0’s is simple to see. If 0.000010101 is divided by 0.10111 It is easy to see that the first four quotient bits are zero. So rather than performing the subtraction, the dividend is renormalized each time a string of zero’s is encountered. Similarly, if after each subtraction the result is a string of 1’s, then the 1’s can be skipped over placing 1’s in the quotient bit. This technique is derived in Problem 4.5.

4.4.4 Newton’s Method

In Newton’s method the quotient to be formed is the product A (1 / B). For this case, once 1 / B is determined a single multiplication cycle generates the desired result. Newton’s method yields the iteration

which for the function

gives

Under suitable well known conditions x_i will converge to the inverse. Hence using Newton’s algorithm the process of division is achieved via addition and multiplication operations. The C++ source code illustrating this technique is shown in Code List 4.17. The output of the program is shown in Code List 4.18.

Code List 4.17 Floating Point Division

Code List 4.18 Output of Program in Code List 4.17

4.5 Residue Number System

4.5.1 Representation in the Residue Number System

The residue number systems is a system which uses an alternate way to represent numbers. For integers, in 2’s complement notation, the representation for a number was

with a value of

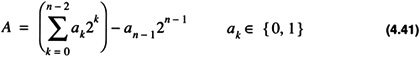
For this case, a number A is represented with n binary bits. The value is relatively easy to calculate via Eq. 4.41. A natural problem occurred with this representation for the process of addition. When n is large the calculation of the carry-in to each stage is the dominating factor with regard to the performance of the addition operation as noted in Section 4.1.2. Using methodologies in number theory, an alternate representation can be used which reduces the problems of with regard to the carry-in calculation.

The residue number system uses a set of relatively prime numbers:

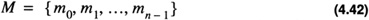
and represents a number A with respect to these moduli by the n-tuple:

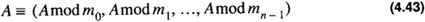
Two numbers are relatively prime if their greatest common divisor is one. Using the standard notation with

to denote the greatest common divisor of x and y. The requirement on the set M is that each of the members be pairwise relatively prime:

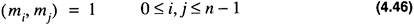
For example, a representation with the moduli

the number 12 is represented as

and 14 is represented as

The addition of 12 and 14 can be accomplished by adding the vector representation and performing the modulus operation:

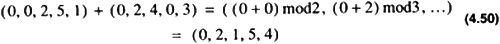
Notice that the result is the same obtained when representing 26 in the notation.

The Range of the Residue Number Systems

The residue number system can represent N distinct numbers with

For example, the moduli in Eq. 4.47,

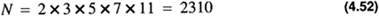
The result stated in Eq. 4.51 is established in Problem 4.15.

4.5.2 Data Conversion — Calculating the Value of a Number

This section derives a method for calculating the value of a number given only its representation in terms of the moduli. It is necessary to introduce some quantities in number theory. The Euler totient function, φ (n) , is defined for a number, n, as the number of positive integers satisfying

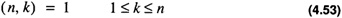
For example,

If n is a prime number then

defining the weights, w_i, as

The vector W as

and a number A, as

The value of A is given as

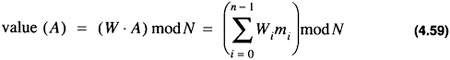
This result is established in Problem 4.17. Consider the example in Eq. 4.47. For this case:

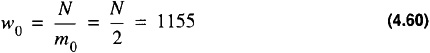
Similarly, W becomes

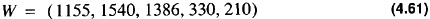
To calculate the number 26 from its representation in Eq. 4.50 one has

4.5.3 C++ Implementation

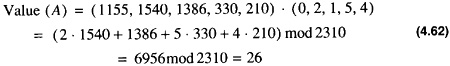
A program to simulate the Residue Number System is shown in Code List 4.19. The output of the program is shown in Code List 4.20.

In the program a class data is declared which has the following data and functions:

•  unsigned moduli[N]: this data item is used to hold the representation of each of the moduli.

•  data: this is the constructor function for data which is called any time a variable is declared.

•  set: this function is used to set the data’s value.

•  print: this function is used to print out the moduli and the value by calling the value function.

•  value: this function calculates the value of the number from its residue representation.

•  operator+: the + operator has been overloaded to perform the required addition in the residue number system.

•  operator*: the * operator has been overloaded to perform multiplication in the residue number system.

This program is a natural example for the use of the overloading operators in C++. Since the addition of the two numbers in the residue systems consists of the respective additions of their moduli it is natural to replace this operator for addition.

The output supplies all the moduli and prints out the relatively prime numbers at the top. Notice that the print function takes in an optional char * to print out a small string. If the string is not supplied it defaults to an empty string.

Code List 4.19 Residue Number System

Code List 4.20 Output of Program in Code List 4.19

Code List 4.21 Euler Totient Function

Code List 4.22 Output of Program in Code List 4.21