Algorithms and Data Structures in C++ by Alan Parker CRC Press, CRC Press LLC ISBN: 0849371716   Pub Date: 08/01/93

3.5 Operations on Linked Lists

There are a number of operations on linked lists that are useful. These operations might be assigned to a class from which different types of linked lists are derived. Some common operations might be

•  add_object — to add an object to the linked list

•  destroy_object — to destroy an object of the linked list

•  find_Object — to find an object in the list

•  find_member — to search the whole list for a specific member

•  find_last-member — finds the last object in the list which matches the specific member

A number operations including sorting might also be defined for the linked list.

3.5.1 A Linked List Example

This section presents a complete example in C++ which demonstrates the use of linked lists to search for the solution to a particular coffee-house game. The purpose of the game is to eliminate as many pegs as possible on a triangular board by jumping individual pegs. The board used for this example consists of ten slots and nine pegs. The board is numbered and initialized as shown in Figure 3.9. Initially, the nine pegs occupy slots one through nine and slot zero is unoccupied. A peg may jump an adjacent peg (horizontally, or diagonally) into an unoccupied slot. The peg that is jumped is removed from the board. This is similar to capturing a piece by jumping in the game of checkers.

A valid move sequence produced by the program in Code List 3.19 is illustrated in Figure 3.9. The first move in the game is for peg number five to jump over peg number two landing in the empty slot zero. Peg number two is removed from the board and the game continues. The next move is to move peg number seven, jumping over peg number four, and landing in the unoccupied slot two. Peg number four is then removed from the board. The game continues in a similar fashion until there are no more possible moves. At the end of the game in Figure 3.9 three pieces remain on the board: piece number five, piece number six, and piece number eight.

The output of the program is shown in Code List 3.20. The output presents an X if there is a peg remaining at a specific position and a 0 if there is no peg. As seen in the output file at the stage the search is printed out there are three pegs left for each combination. The output is the exhaustive list of all combinations which result in three pegs remaining after six moves. In all cases there are no more additional valid moves. The paths are printed for each solution. Multiple paths give rise to the same final peg distribution for instance

[(5,0),(7,2),(0,5),(9,7),(6,8),(1,6)]

and

[(5,0),(7,2),(9,7),(6,8),(1,6), (0,5)]

both result in 00000XX0X0.

One of the problems with the program is the massive amount of data required to store all valid paths which lead to a fixed peg configuration. Consider the problem of expanding the game to the “real” coffee house game which really consists of 14 pegs initially placed on a triangle. If the program is modified to support the new triangle then it requires too much memory to run on most workstations. As a result if the desired problem is to find one path that is optimal a different approach described in the next section must be taken.

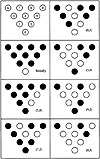
Figure 3.9  A Particular Game Sequence

3.5.1.1 Bounding a Search Space

In order to minimize the arbitrary expansion of paths for the coffee house game of size 15 the program can be modified to remove any entries in the linked list which duplicate a configuration obtainable via another path. If this approach is taken then only one path will be saved at each point in the iteration for a given intermediate position. This will bound the search space at each iteration and will result in a workable solution. Using a rather unsophisticated argument it is easy to see that the amount of memory is reduced significantly and is realistically bounded. Since each position is represented as a sequence of 15 0’s and X’s the maximum number of positions under consideration at any time is 215. For each position only one path is stored instead of the myriad of paths which result in the same position. This approach is used in Problem 3.6 to find a solution for the coffee house game.

Code List 3.19 Source Code for Game Simulation

Code List 3.20 Output of Program in Code List 3.19

3.6 Linear Search

A linear search is a search which proceeds in a linear fashion through a list.

The C++ code to perform a linear search on strings is shown in Code List 3.21. The output of the program is shown in Code List 3.22

Code List 3.21 Linear Search Code for Strings

Code List 3.22 Output of Program in Code List 3.21

3.7 Binary Search

The binary search is used in a sorted array to search for an element. The search consists of comparing against the middle of the list and proceeding to search the higher or lower sublist in a recursive fashion.

A binary search is shown in C++ in Code List 3.23. The output is shown in Code List 3.24. A binary search for strings is illustrated in Code List 3.25. The output of the program is shown in Code List 3.25.

Code List 3.23 Binary Search for Integers

Code List 3.24 Output of Program in Code List 3.23