
by Alan Parker
CRC Press, CRC Press LLC
ISBN: 0849371716 Pub Date: 08/01/93

|
Algorithms and Data Structures in C++
by Alan Parker CRC Press, CRC Press LLC ISBN: 0849371716 Pub Date: 08/01/93 |
| Previous | Table of Contents | Next |
The quick sort algorithm is a simple yet quick algorithm to sort a list. The algorithm is comprised of a number of stages. At each stage a key is chosen.
Code List 3.25 Binary Search for Strings
The algorithm starts at the left of the list until an element is found which is greater than the key. Starting from the right, an element is searched for which is less than the key. When both the elements are found they are exchanged. After a number of iterations the list will be divided into two lists. One list will have all its elements less than or equal to the key and the other list will have all its elements greater than or equal to the key. The two lists created are then each sorted by the same algorithm.
Code List 3.26 Output of Program in Code List 3.25
The internal details of a quicksort algorithm are shown in the C++ program in Code List 3.27. The output of the program is shown in Code List 3.28.
A number of different approaches can be used to determine the key. The quicksort algorithm in this section uses the median of three approach. In this approach a key is chosen for each search segment.
The key is given as the median of three on the bounds of the segment. For instance, in Code List 3.28, the initial segment to sort contains 18 elements, indexed 0-17. The first key is determined by the calculation
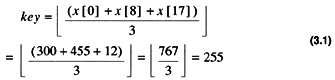
After the comparisons two lists are formed. In this case the lists are 0-8 and 9-17. Every element in the first list will be less than or equal to the key 255 and everything in the second list will be greater than or equal to 255. The two new lists can be sorted in parallel. This example is sequential code so that the second list 9-17 is dealt with first.
The comparisons occurring within the first list is illustrated in Code List 3.29. Two comparisons can be done in parallel. Starting from the left a search is made for the first element greater than 255. In this case the first element satisfies that criteria.
Starting from the right a search is made for the first element that is less than 255. In this case it is the last element. At this point the two elements are exchanged in the list which results in the second list in Code List 3.29. Continuing in this manner proceeding from the left the next element in the list is searched for which is greater than 255. In this case it is the third element in the list, 415. Proceeding from the right the first element less than 255 found is 100. Again, 100 and 415 are exchanged resulting in the third list. Eventually the two left and right pointers overlap indicating that the list has been successfully sorted about the key.
C++ also provides a quicksort operator which performs the median of three sort. This is illustrated for strings is illustrated in Code List 3.34. The output of the program is shown in Code List 3.35 A quicksort C++ program for doubles is shown in Code List 3.30 The output is shown in Code List 3.31. A quicksort program for integers is shown in Code List 3.32. The output is shown in Code List 3.33.
Code List 3.27 QuickSort C++ Program
Code List 3.28 Output of Program in Code List 3.27
Code List 3.29 QuickSort Comparison
Code List 3.30 QuickSort For Double Types
Code List 3.31 Output for Program in Code List 3.30
Code List 3.32 QuickSort Program for Integers
Code List 3.33 Output for Program in Code List 3.32
Code List 3.34 QuickSort Program
Code List 3.35 Output of Program in Code List 3.34
A binary tree is a common data structure used in algorithms. A typical class supporting a binary tree is
class tree
{
public:
int key;
tree * left;
tree * right;
}
A binary tree is balanced if for every node in the tree the height of the left and right subtrees are within one.
There are a number of algorithms for traversing a binary tree given a pointer to the root of the tree. The most common strategies are preorder, inorder, and postorder. The preorder strategy visits the root prior to visiting the left and right subtrees. The inorder strategy visits the left subtree, the root, and the right subtree. The postorder strategy visits the left subtree, the right subtree, followed by the root. These strategies are recursively invoked.
Hashing is a technique in searching which is commonly used by a compiler to keep track of variable names; however, there are many other useful applications which use this approach. The idea is to use a hash function, h (E) , on elements, E , to assist in locating an element. For instance a dictionary might be defined using an array of twenty six pointers, D [26] . Each pointer points to a linked list of data for the specific letter of the alphabet. The hashing function on the string simply returns the number of the letter of the alphabet minus one of the first characters in the string:

There are two major operations which need to be supported for the hash table created:
The idea of hashing is to simplify the search process so the hashing function should be simple to calculate. Additionally, there should be a simple way to locate the data, referred to as resolving collisions, once the hash function is evaluated.
The simulated annealing algorithm is illustrated in Figure 3.10. The goal of simulated annealing is to attempt to find an optimum to a large-scale problem which typically cannot be found by conventional means. The solution is sought by iterating and evaluating a cost at each stage. The algorithm maintains a concept of a temperature. When the temperature is high the algorithm will be likely to accept a higher cost solution. When the temperature is very low the algorithm will almost always only accept solutions of lower cost. The temperature begins high and is cooled until an equilibrium is reached. By allowing the initial temperature to be high the algorithm will be allowed to “climb hills” to seek a global optimum. Without this feature it is possible to be trapped in a local minimum. This is illustrated in Figure 3.12. By allowing the function to move to a higher value it is able to climb over the hill and find the global minimum.
Simulated annealing is applied to the square packing problem described in the next section. This illustrates the difficulty and complexity of searching in general problems.
| Previous | Table of Contents | Next |