
by Alan Parker
CRC Press, CRC Press LLC
ISBN: 0849371716 Pub Date: 08/01/93

|
Algorithms and Data Structures in C++
by Alan Parker CRC Press, CRC Press LLC ISBN: 0849371716 Pub Date: 08/01/93 |
| Previous | Table of Contents | Next |
This section presents the principles of addition, multiplication and division for fixed point 2’s complement numbers. Examples are provided for a selection of important fixed point algorithms.
Two’s complement addition generates the sum, S, for the addition of two n-bit numbers A and B with
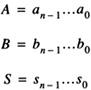
A C++ program simulating 8-bit two’s complement addition is shown in Code List 4.1. The output of the program is shown in Code List 4.2
Code List 4.1 2’s Complement Addition
Code List 4.2 Output of Program in Code List 4.1
The programs do not check for overflow but simply simulate the additon as performed by hardware.
In order to develop some fast algorithms for multiplication and addition it is necessary to analyze the process of addition and multiplication at the bit level. Full and half adders are bit-level building blocks that are used to perform addition.
A half adder is a module which inputs two signals, ai and bi, and generates a sum, si, and a carry-out ci. A half adder does not support a carry-in. The outputs are as in Table 4.1.
| Input | Output | ||
|---|---|---|---|
| ai | bi | si | ci |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
A full adder has a carry-in input, ci. A full adder is shown in Table 4.2.
| Input | Output | |||
|---|---|---|---|---|
| ai | bi | ci-1 | si | ci |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
The full adder and half adder modules are shown in Figure 4.1. The boolean equation for the output of the full adder is
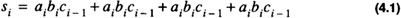
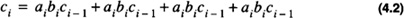
The boolean equation for the output of the half adder is
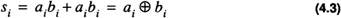
where ⊕ denotes the exclusive-or operation.

The output delay of each module can be expressed in terms of the gate delay, Δ, of the technology used to implement the boolean expression. The sum, si, for the full adder can be implemented as in Eq. 4.1 using four 3-input NAND gates in parallel followed by a 4-input NAND gate. The gate delay of a k-input NAND gate is Δ so the sum is calculated in 2Δ. This is illustrated in Figure 4.2. For the half-adder the sum is calculated within I Δ and the carry is generated within I Δ.The Output Delay for the Half Adder is shown in Figure 4.2.
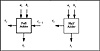
Figure 4.1 Full and Half Adder Modules
2’s complement addition of n-bit numbers can be performed by cascading Full Adder modules and a Half Adder module together as shown with a 4-bit example in Figure 4.3. The carry-out of each module is passed to the carry-in of the subsequent module. The output delay for an n-bit ripple-carry adder using a Half Adder module in the first stage is
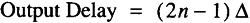
For many applications this delay is unacceptable and can be improved dramatically.
A C++ program to perform ripple carry addition is shown in Code List 4.3. The output of the program is shown in Code List 4.4. The program demonstrates the addition of 1 + (-1). As can be seen in the output the carry ripples through the result at each simulation until it has passed over N bits.
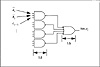
Figure 4.2 Output Delay Calculation for a Full Adder
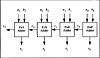
Figure 4.3 2’s Complement 4-Bit Adder
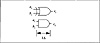
Figure 4.4 Output Delay Calculation for a Half Adder
Code List 4.3 Ripple Carry Addition
Code List 4.4 Output of Program in Code List 4.3
The addition of two numbers may result in an overflow. There are four cases for the generation of overflow in 2’s complement addition:
Overflow is not possible when adding numbers with opposite signs. Overflow occurs if two operands are positive and the sum is negative or two operands are negative and the sum is positive. This results in the boolean expression
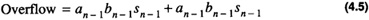
| Previous | Table of Contents | Next |