
by Alan Parker
CRC Press, CRC Press LLC
ISBN: 0849371716 Pub Date: 08/01/93

|
Algorithms and Data Structures in C++
by Alan Parker CRC Press, CRC Press LLC ISBN: 0849371716 Pub Date: 08/01/93 |
| Previous | Table of Contents | Next |
An example of booth recoding is illustrated in Table 4.5. In the worst case the Booth algorithm requires that n operations be performed to compute the product. This is illustrated in the last entry in Table 4.5. As a result the recoding operation for this operand has not simplified the problem. The average number of operations for a random operand by the algorithm is determined in Problem 4.10. Due to the average and worst-case complexity of the Booth algorithm a better solution is sought to find the product.
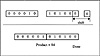
Figure 4.14 Booth Algorithm
| Original Number | Booth Recode | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | -1 |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | -1 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | -1 | 1 | -1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 |
| Bit Pattern | Operation | |
|---|---|---|
| 0 | 0 | product unchanged |
| 0 | 1 | product += a |
| 1 | 0 | product -=a |
| 1 | 1 | product unchanged |
Code List 4.11 Booth Algorithm
Code List 4.12 Output of Program in Code List 4.11
The Bit-Pair recoding technique is a technique which recodes the bits by considering three bits at a time. This technique will require n/2 additions or subtractions to compute the product. The recoding is illustrated in Table 4.7. The bits after recoding are looked at two at a time and the respective operations are performed. The higher order bit is weighted twice as much as the lower order bit. The C++ program to perform bit-pair recoding is illustrated in Code List 4.13. The output is shown in Code List 4.14.
The bit pair recoding algorithm is shown in Figure 4.14. The algorithm is analogous to the Booth recoding except that it investigates three bits at a time while the Booth algorithm looks at two bits at a time. The bit-pair recoding algorithm needs to have access to A, -A, 2A, and -2A and as a result needs another additional 1-bit register to the left of P which is initialized to zero.
| Bit Pattern | Operation | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

Figure 4.15 Bit Pair Recoding Algorithm
Code List 4.13 Bit-Pair Recoding Program
Code List 4.14 Output of Program in Code List 4.13
| Previous | Table of Contents | Next |