
by Alan Parker
CRC Press, CRC Press LLC
ISBN: 0849371716 Pub Date: 08/01/93

|
Algorithms and Data Structures in C++
by Alan Parker CRC Press, CRC Press LLC ISBN: 0849371716 Pub Date: 08/01/93 |
| Previous | Table of Contents | Next |
A simple boolean logic simulator is shown in Code List 4.7. The output of the program is shown in Code List 4.8. The program simulates the interconnection of gates and is used to demonstrate the behavior of a clocked D flip-flop.
The program simulates the behavior of the circuit by calculating new values in the simulation in terms of the old values. The old values are then updated and the process is performed again. The process continues until the new and old values are identical or until a terminal count has been reached. For this program a terminal count of 50 is used but it is never reached in this example.
The circuit that is implemented is shown in Figure 4.11. The program allows each net to have one of three values: 0, 1, or 2. The values are as follows:
All the values in the NET structure are initialized to the unknown state 2. As the inputs, clock, and data propagate through the circuit the values are changed as they become determined.
The behavior of each gate is modelled by its associated function within the program. The gates input one of the three states. The output is determined according to the logical function. This is illustrated in Table 4.4 for the 2-input NAND gate for all nine possibilities of the inputs.
| NAND behavior | ||
|---|---|---|
| x | y | f(x,y) |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | x | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| 1 | x | x |
| x | 0 | 1 |
| x | 1 | x |
| x | x | x |
The output data is shown in the timing diagram in Figure 4.13. As can be seen in the figure the circuit behaves as expected. The Q and QBAR outputs remain unknown until the first rising edge of the clock and at that point the output Q reflects the value of DATA at the clock edge. Only subsequent rising edges of the clock cause the outputs to change. It is important to note that this specific test does not demonstrate the validity of the device as a D flip-flop. In the absence of a theoretical proof a considerable amount of additional testing is necessary.
There is another interesting point about the simulation which can cause problems in circuit design. By looking at the last clock rise in Code List 4.8 one notes that QBAR makes a zero to one transition one gate delay quicker than Q making the corresponding one to zero transition. This is illustrated in Figure 4.12. As a result, it is important to let the data stabilize prior to its use.
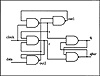
Figure 4.11 D Flip-Flop Circuit for Simulation
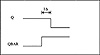
Figure 4.12 Transition Timing
The goal of this section is to investigate algorithms for fast multiplication of two n-bit numbers to form a product. If two’s complement notation is used
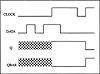
Figure 4.13 Timing Diagram for Simulation
Code List 4.7 Boolean Logic Simulator
Code List 4.8 Output of Program in Code List 4.7
then when multiplying two numbers, A and B,


In order to store the result one needs to calculate the number of bits required to represent the product in 2’s complement form. By noting the range of 2’s complement from Table 1.4 on page 11 one obtains that 2n bits are required in 2’s complement form. The product is formed as

Since 2n bits are stored in the hardware for the product then overflow is not an issue.
The shift-add technique is the simple grade school technique for multiplication. In this scenario a partial product is formed by adding as appropriate repeated shifts of the multiplicand. The core statement in Code List 4.9 is
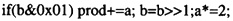
This statement forms the product by repeatedly evaluating the lsb of the multiplier and if it is set by adding the shifted multiplicand. At each iteration the multiplier is shifted right to investigate the next bit and the multiplicand is shifted left.
Code List 4.9 Shift Add Technique
Code List 4.10 Output of Code List 4.9
The Booth algorithm is a recoding technique which attempts to recode the multiplier to speedup the scenario where there are sequences of 1’s. As an example consider the multiplication in base 10 of 9999*7. One can evaluate the result rather quickly by performing (10000-1)*7=69993. This can be done without the assistance of a computing device. The algorithm used is to recode the sequence of 9’s and results in an operation which is much simpler. The technique can also be applied in binary. Instead of sequences of 9’s however, one is interested in sequences of 1’s.
The Booth algorithm is illustrated in Figure 4.14. In the figure the product is formed as the multiplication of A and B (A=14 and B=6). When the result is done A remains unchanged and the product is formed in P:B where the : operator indicates register concatenation. Register B no longer contains its initial value. This is written as

The destruction of register B is common because it uses one less register to form the product. The Booth algorithm considers the lower order bit of register B in conjunction with the added bit which is initialized to zero. The bits determine the operation according to Table 4.6.
| Previous | Table of Contents | Next |